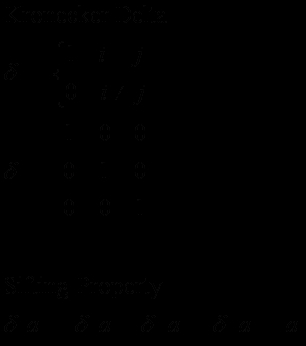Come calcoli matematici più complessi, le equazioni diventano più onerose. Scalari notazione denota solo magnitudo, mentre un vettore rappresenta una grandezza e una direzione. In matematica più avanzata, gli scienziati e gli ingegneri utilizzano tensori per la notazione. Un tensore rappresenta un ordine di grandezza e di due o più direzioni, che include scalari e vettoriali entità. Un tensore di ordine zero è un valore scalare, un tensore di primo ordine è un vettore e un tensore di secondo ordine è una matrice.
Notazione
Un tensore di secondo ordine generale utilizza una variabile con tre pedice, che di solito sono "io", "j" e "k." Alcuni avanzata fisica o altre applicazioni scientifiche superiori possono richiedere tensori sopra secondo ordine, ma la maggior parte delle applicazioni richiedono solo un secondo ordine o qui sotto. Ogni indice rappresenta il numero di dimensioni, che di solito è tre. Un tensore di ordine zero non ha nessun pedici, un primo ordine ha uno e un secondo ordine ha due. Questo modello continua nei tensori di ordine superiore.
Delta di Kronecker
Il delta di Kronecker è tensore speciale che rappresenta la matrice di identità. Il tensore è uguale a uno quando "io" è uguale a "j", ma è zero quando "io" non è uguale a "j." Questo tensore speciale include anche una proprietà "setaccio", secondo la quale la sezione i produce a (j). Solo i termini dove "i" equivale a "j" vengono visualizzati nel grafico, poiché gli altri termini sono tutti pari a zero per definizione.
Prodotto di puntino di vettore
Al fine di essere utile, che un tensore ha per di più che semplicemente rappresentare una certa quantità..--deve anche essere in grado di rappresentare un calcolo. Un'operazione matematica comune è il prodotto di puntino del vettore, o il prodotto interno. Questa operazione viene da una derivazione che coinvolgono il delta di Kronecker. Il grafico illustra due Delta di Kronecker essere moltiplicati tra loro. L'ultima riga di quell'equazione corrisponde la definizione di un prodotto di puntino di vector, in modo che una notazione tensoriale utilmente raffigura un prodotto di puntino di vector.
Alternando il tensore
Il tensore alternato è un altro tensore speciale progettato per rendere possibili alcune operazioni matematiche. Come la delta di Kronecker, il valore del tensore alternante è condizionale sul suoi indici, ma dove il delta di Kronecker ha due indici, il tensore alternato ha tre. I valori uguali a zero consentono un'operazione di prodotto incrociato quando combinato con due tensori di primo ordine.
Simmetria
Un tensore simmetrico è uno in cui t(i,j) = t(j,i). Un tensore anti-simmetrico in cui t (i, j) = - t(j,i). Ogni tensore può essere espresso come una mezza la somma di un tensore simmetrico e un tensore anti-simmetrico. Nello spazio tridimensionale (cartesiano), qualsiasi vettore può trasformarsi in un tensore anti-simmetrico utilizzando il vettore alternativo. Nel grafico, omega(k) è il vettore e R(i,j) è il tensore.