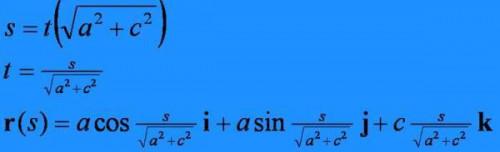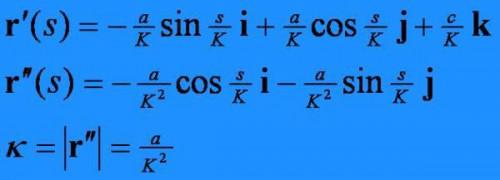Curvatura, lunghezza dell'arco e torsione sono tre proprietà scalari di curve tridimensionali. Lunghezza dell'arco è la distanza lungo una curva. La curvatura è una misura di quanto un arco curve a raggio stretto, o quanto si discosta da un vettore tangente in un qualsiasi punto lungo l'arco. La torsione è una misura di quanto una curva colpi di scena in tre dimensioni. È necessario conoscere come calcolare il vettore dot prodotti e prodotti trasversali per calcolare la torsione. Si deve anche essere in grado di calcolare integrali e derivate semplice.
Istruzioni
•
Calcolare la funzione di lunghezza arco della curva, che è un'elica in questo esempio. Prendere il primo derivato del vettore curva e quindi calcolare il prodotto scalare del vettore derivato primo con se stesso. Prendere l'integrale da "0" a "t" della radice quadrata del prodotto di puntino. La variabile "a", "t" è stato introdotto come variabile di integrazione, poiché "t" rappresenta un limite per l'integrazione.
Trasformare il vettore "r" in un vettore del parametro "s". Dal momento che "s" è la lunghezza dell'arco, risolvere l'equazione di lunghezza di arco per "t" e quindi sostituire il risultato in "r" per ottenere "r."
• Calcolare il vettore tangente di unità. Questo vettore è uguale alla derivata prima della "r". La notazione è più pulita con l'aggiunta della variabile "K" come mostrato.
Calcolare la curvatura, che è la grandezza della derivata seconda di "r." Anche questo è uguale al primo derivato del vettore tangente unità.
• Calcolare i vettori normali di due unità. Il principale vettore unitario perpendicolare, "Jacobiana," è la derivata seconda della "r" diviso per la curvatura. Il vettore binormale unitario, "b(s)," è il prodotto trasversale di vettore tangente unitario, "u(s)" e il principale vettore normale di unità.
Calcolare la torsione. Prendere il primo derivato dell'unità vettore binormale. Calcolare il prodotto di puntino del negativo del vettore normale unità principale, "-Jacobiana," e il primo derivato del vettore binormale unità, "b'(s)." Questo valore è la torsione della curva.